Matrizes¶
Strings, Tuplas e Listas são exemplos de sequências em Python, representando coleções unidimensionais. Matrizes, por sua vez, são estruturas bidimensionais organizadas em linhas e colunas, a exemplo de:
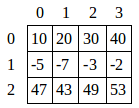
na qual há 3 linhas e 4 colunas.
Strings, Tuplas e Listas são exemplos de sequências em Python, representando coleções unidimensionais. Matrizes, por sua vez, são estruturas bidimensionais organizadas em linhas e colunas, a exemplo de:

na qual há 3 linhas e 4 colunas.
# Construção de uma estrutura bidimensional (matriz) de 3x4
matriz = [[10, 20, 30, 40],
[-5, -7, -3, -2],
[47, 43, 49, 53]]
print(matriz)
# Construção de uma estrutura bidimensional (matriz) de 3x4, com valor 0 (zero) em todas as células
n = 3
m = 4
matriz = [ [0] * m for _ in range(n)]
print(matriz)
Como temos duas dimensões, são necessários dois índices para identificar um elemento específico na matriz. Por convenção, em geral o primeiro índice identifica a linha, enquanto que o segundo índice identifica a coluna
# Ober o segundo elemento' (índice 1) da terceira linha (índice 2)
x = matriz[2][1] * 45
# Obter o último elemento da matriz (último elemento da última linha)
print( matriz[-1][-1] )
# Alterar o valor de uma posição da matriz utilizando operador de atribuição
x = 13
i = 1
j = 2
matriz[2][0] = 500 * x
matriz[i][j] = matriz[i+1][j+1] - 5
matriz[i][j] += x
print(matriz)
Em realidade, a construção da matriz acima faz uso de um recurso disponível em Python chamado de aninhamento de estruturas de dados, ou seja, a possibilidade de um elemento de uma lista ser uma outra lista (ou uma tupla.
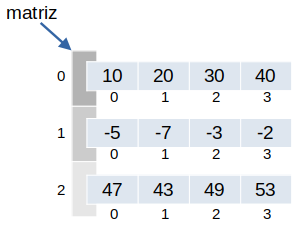
Essa noção é importante para compreender algumas operações sobre essa estrutura.
Uma forma alternativa de trabalhar com matrizes em Python é via módulo Numpy
# Pegar a segunda linha (uma lista) da matriz
linha = matriz[1]
print(linha)
# Obter o número de linhas da matriz (tamanho da primeira dimensão)
print(len(matriz))
print(len(matriz[0]))
Para obter o número de colunas da matriz (tamanho da segunda dimensão) basta pegarmos o tamanho de qualquer uma das 3 listas que definem as linhas.
# Obter o número de colunas da matriz (tamanho da segunda dimensão)
# que corresponde ao tamanho de qualquer de suas linhas
print(len(matriz[0]))
print(len(matriz[1]))
print(len(matriz[2]))
Como trata-se de estruturas aninhadas, os elementos de cada lista (as linhas) podem ter tamanho distintos. Os valores podem, também, ser de tipos distintos.
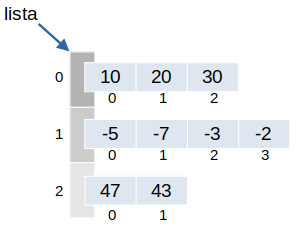
# Uma estrutura bidimensional cujas linhas possuem quantidades diferentes de elementos
bi = [[10, 20, 30], [-5, -7, -3, -2], [47, 43]]
print(len(bi))
print(len(bi[0]))
print(len(bi[1]))
print(len(bi[2]))
# Matriz como elementos não homogêneos
lista1 = [ ["Huguinho", "Zézinho", "Luizinho"],
[10, 50],
[3.14, 2.15] ]
print(lista1)
# Uma lista de duplas
lista2 = [(4, 5), (5, 15), (-5, 10)]
print(lista2)
#i Imprimir o primeiro elemento da última dupla
print(lista2[-1][0])
# Lendo uma matriz
# A primeira linha tem dois valores inteiros n e m correspondentes as dimensões da matriz
# Em seguinda vem n linhas, cada uma delas com os m valores que definem cada linha
n, m = [int(x) for x in input().split()]
matriz = []
for _ in range(n):
matriz.append([int(x) for x in input().split()])
# Lendo uma matriz
# O código acima pode ser escrito de forma mais sintética como:
n, m = [int(x) for x in input().split()]
matriz = [[int(x) for x in input().split()] for _ in range(n)]
# Imprimir a matriz, linha a linha
matriz = [ [10, 15, 18], [7, 5, 3]]
for linha in matriz:
print(*linha)
# Somar todos os elementos da matriz
# Percorrer todas as linhas, e para cada linha percorrer a lista correspondente às colunas
matriz = [ [10, 15, 18], [7, 5, 3]]
soma = 0
for linha in matriz:
for x in linha:
soma += x
print(soma)
# Somar todos os elementos da matriz
# O código acima pode ser escrito de forma mais sintético como:
matriz = [ [10, 15, 18], [7, 5, 3]]
soma = 0
for linha in matriz:
soma += sum(linha)
print(soma)
# Somar todos os elementos da matriz
# O código acima pode ser escrito de forma aindA mais sintético como:
matriz = [ [10, 15, 18], [7, 5, 3]]
soma = sum( sum(linha) for linha in matriz )
print(soma)
# Somar todos os elementos da matriz
# Com percorrimento das linhas e para cada linha de seus valores (as colunas) baseado nos índices.
matriz = [ [10, 15, 18], [7, 5, 3]]
soma = 0
for i in range(len(matriz)):
for j in range(len(matriz[i])):
soma += matriz[i][j]
print(soma)
# Somar todos os elementos da matriz
# Agora com percorrimento das colunas e para cada coluna de seus valores (as linhas) baseado nos índices.
matriz = [ [10, 15, 18], [7, 5, 3]]
soma = 0
for j in range(len(matriz[0])):
for i in range(len(matriz)):
soma += matriz[i][j]
print(soma)
Em matemática, matriz transposta é a matriz que se obtém pela troca (transposição) de linhas por colunas de uma dada matriz.
Uma matriz:
| 10 | 20 | 30 |
| 5 | 6 | 7 |
Sua transposta:
| 10 | 5 |
| 20 | 6 |
| 30 | 7 |
#Obter a matriz transposta
matriz = [ [10, 20, 30], [5, 6, 7] ]
num_linhas = len(matriz)
num_colunas = len(matriz[0])
transposta = [ [0] * num_linhas for _ in range(num_colunas) ]
for i in range(num_linhas):
for j in range(num_colunas):
transposta[j][i] = matriz[i][j]
print(transposta)
Sudoku é um jogo de lógica cujo objetivo é distribuir números de 1 a 9 em cada uma das células numa grade de 9x9 de tal forma que não haja repetição de um desses números em cada uma das linha, em cada uma das colunas ou em cada uma das subgrades (regiões) de 3x3 do tabuleiro.
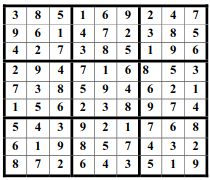
O tabuleiro acima apresenta uma possível solução para esta distribuição. Desejamos, agora, verificar se de fato esta distribuição de números atende às restrições acima mencionadas.
def verifica_tabuleiro(tabuleiro):
#Verifica se há repetição de número nas linhas
for lin in range(9):
c = set( tabuleiro[lin] )
if len(c) != 9:
return False
# Verifica se há repetição de número nas colunas
for col in range(9):
c = set( tabuleiro[lin][col] for lin in range(9) )
if len(c) != 9:
return False
# Verifica se há repetição de número nas subgrades de 3x3
for lin in range(0, 9, 3):
for col in range(0, 9, 3):
c = set()
for l in range(lin, lin+3):
c.update(tabuleiro[l][col:col+3])
if len(c) != 9:
return False
return true
# Lê os números do tabuleiro de Sudoku
tb = [ [int(x) for x in input().split()] for _ in range(9) ]
sudoku_ok = verifica_tabuleiro(tb)
print(sudoku_ok)