Conjunção: E (∧)¶
- a > 5 ∧ b = 7
Nesta expressão temos duas subexpressões relacionais:
- p: a > 5
- q: b = 7
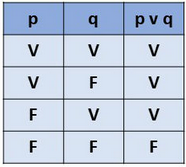
cada uma delas resultando num valor lógico (Verdade ou Falso). Estes valores lógicos são, então, combinados por meio do conectivo lógico E (conjunção), cujo resultado é expresso na tabela abaixo:

Em Python esta expressão pode ser expressa por:
- a > 5 and b == 7