O que é uma variável?

Em geral

De forma geral, uma variável pode ser entendida como uma classificação ou uma medida; uma quantidade que se altera em cada caso ou unidade de estudo. Uma propriedade no objeto de estudo que pode ser medida e enumerada." (InfoEscola)

A título de exemplo, suponha que estejamos analisando um grupo de pessoas do ponto de vista econômico. Neste caso podemos estar interessado em classificar ou medir as pessoas considerando variáveis como:

• renda: valor mensal resultante da da atividade econômica da pessoa
• estado civil: se a pessoa é solteira, casada, etc
• idade: quantos anos a pessoa tem

Já no contexto de uma empresa de seguros de veículos, as variáveis que podem interessar para efeito de análise e cálculo de seguro são:

• marca do veículo
• ano de fabricação do veículo
• idade do principal condutor
• endereço residencial (se pessoa física)
• característica de garagem (aberta, fechada, coberta, etc)

Na matemática

Na matemática elementar, uma variável é um símbolo (geralmente uma única letra) que representa um número arbitrário, não totalmente especificado ou desconhecido (wikpedia. É uma quantidade que pode mudar no contexto de um problema ou experimento.

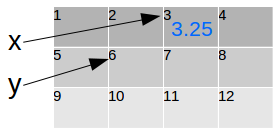
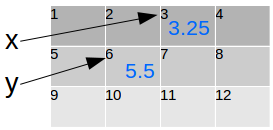
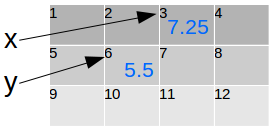
Por convenção, em geral as primeiras letras do alfabeto, a, b, c etc são usadas para representar quantidades conhecidas (coeficientes), enquanto as últimas letras do alfabeto, x, y, z, são usadas para representar quantidades desconhecidas. Mas por vezes são utilizadas letras que lembram-nos a quantidade que ela representa, como é to caso de t para tempo, v para velocidade, etc.

O uso de variáveis como se fossem número explícitos possibilita generalizar a resolução de problemas, como é o caso da resolução (cálculo das raízes) de equações de segundo grau como ax² + bx + c = 0, cujos valores podem ser obtidos pela fórmula de Bhaskara:

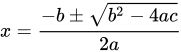
Assim, conhecidos os valores dos coeficientes a, b e c de uma equação de segundo grau podemos determinar as raízes, como no caso da equação: 4x² - 4x - 24 = 0 para a qual os valores de x (as raízes) são 3 e -2.

Na computação

Do ponto de vista de um programa de computador, sob certo sentido a noção de variável é similar ao exposto acima. Contudo, estritamente falando uma variável identifica uma posição (endereço) na memória do computador na qual podemos armazenar (guardar) um dado durante um determinado espaço de tempo. Uma métafora comum para representar esta situação é exemplficada no desenho abaixo no qual a memória do computador é vista como uma espécie de conjunto de escaninhos onde cada célula possui um identificar (endereço) único, exemplificao na imagem abaixo pelo números de 1 a 12:

Operador de atribuição (=)

Considere a frase:

Sejam a=4, b=-4 e c=-24, então calcule as raízes da correspondendente equação de segundo grau utilizando a fórmula de Bhaskara

Observe que nesse contexto os coeficientes (variáveis) *a, b* e *c* passam a denotar valores específicos, fato que nos permite retornar à fórmula descrita anteriormente e substituir as variáveis pelos correspondentes valores e, assim, calcular os valores de *x. Dizemos que foram atribuídos* valores às variáveis *a, b* e *c*.

De forma similar, se em Python escrevermos uma expressão como:

x = 3.25

dizemos que está sendo atribuído o valor 3.25 à variável *x, ou seja, que doravante deve-se considerar este valor em todos os cálculos nos quais x* aparecer. Em termos de memória do computador, significa que o valor 3.25 é armazenado no escaninho endereçado por *x*.

Se em seguida escrevermos uma expressão como:

y = 2 * x - 1

inicialmente é resolvida a parte à direita do símbolo de atribuição (=), de form que dado o valor 3.25 atribuído anteriormente a x teremos:

2 * x - 1 = 2 * 3.25 - 1 = 5.5

sendo, então, o valor 5.5 atribuído à variável *y*, resultando em:

# Atribuindo um valor específico à variável x

x = 3.25

# Computando um valor (resolvendo a expressão) e, então, atribuindo o resultado à variável y

y = 2 * x - 1

Note que uma uma expressão envolvendo o operador de atribuíção (*=*) segue a forma:

variável = expressão

ou seja, à esquerda do operador de atribuição (símbolo *=*) devemos sempre encontrar o nome de uma variável, enquanto que à direita podemos ter uma expressão qualquer. A expressão da direita é inicialmente resolvida, sendo o correspondente resultado então atribuído posteriormente à variável.

Sendo assim, é possível escrevermos uma expressão como:

x = x + 4

Apesar de matematicamente esta expressão parecer absurda, do ponto de vista computacional ela é significativa. Seguindo a mesma lógica acima, inicialmente a expressão da direita é resolvida

x + 4 = 3.25 + 4 = 7.25

Em seguida o valor obtido (7.25) é atribuido à variável *x*, fazendo com que seu valor anterior seja perdido.

x = x + 4

Operações desta natureza são relativamente frequentes, de forma que há "atalhos" para elas. A exemplo de outras linguagens de programação, em Python há os operadores +=, -=, *=, /=, //= e %=, conforme exemplificado abaixo.

x = 5

x += 10

# equivalente a: x = x + 10

x -= 3

# equivalente a: x = x - 3

x *= 2

# equivalente a: x = x * 2

x /= 5

# equivalente a: x = x / 5

x //= 5

# equivalente a: x = x // 5

x %= 5

# equivalente a: x = x % 5

Regras para nomes de variáveis em Python

• não podem iniciar com um número

• não podem conter espaços em branco (utilizar _ em vez de branco)

• não podem conter caracteres especiais tais como:

  :'",<>/?|\!@#%^&*~-+
  
  

• é considerada uma boa prática (PEP8) que os nomes de variáveis estejam em letras minúsculas, separadas pelo caracter _ (underscore)

• evite utilizar nomes correspondentes a funções intenas de Python, tais como list e str

• evite utilizar letras como l, O e I uma vez que podem ser confundiadas com 1 and 0

Exemplos de bons nomes de variáveis:

• idade
• salario_minimo
• elemento23